摘要：本文探讨了三角形的中心奥秘，介绍了三角形的性质与特点，包括其几何特性、对称性以及与其他几何图形的关联等。本文还针对用户常见问题进行了详细解答，如如何确定三角形的中心、三角形中心的性质以及在实际应用中的常见问题等。通过阅读本文，读者可以更好地理解三角形中心的奥秘，并解决在实际应用中遇到的常见问题。

性质、特点与应用

在几何学的丰富领域中，三角形中心是一个引人入胜的概念，它涵盖了众多独特且令人着迷的性质和特点，本文将全方位地解读三角形中心的性质，揭示其独特特点，并针对读者常有的疑惑进行解答，旨在帮助大家更好地理解和掌握三角形中心的几何概念，并在实际生活中灵活应用，本文也注重提高文章的搜索引擎友好度，以便更多人了解和探索这一有趣的几何话题。

一、三角形中心的性质

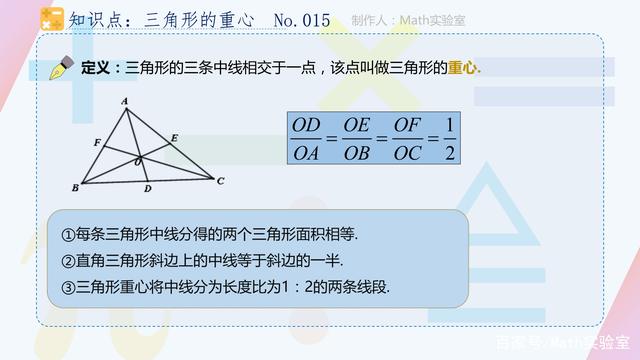
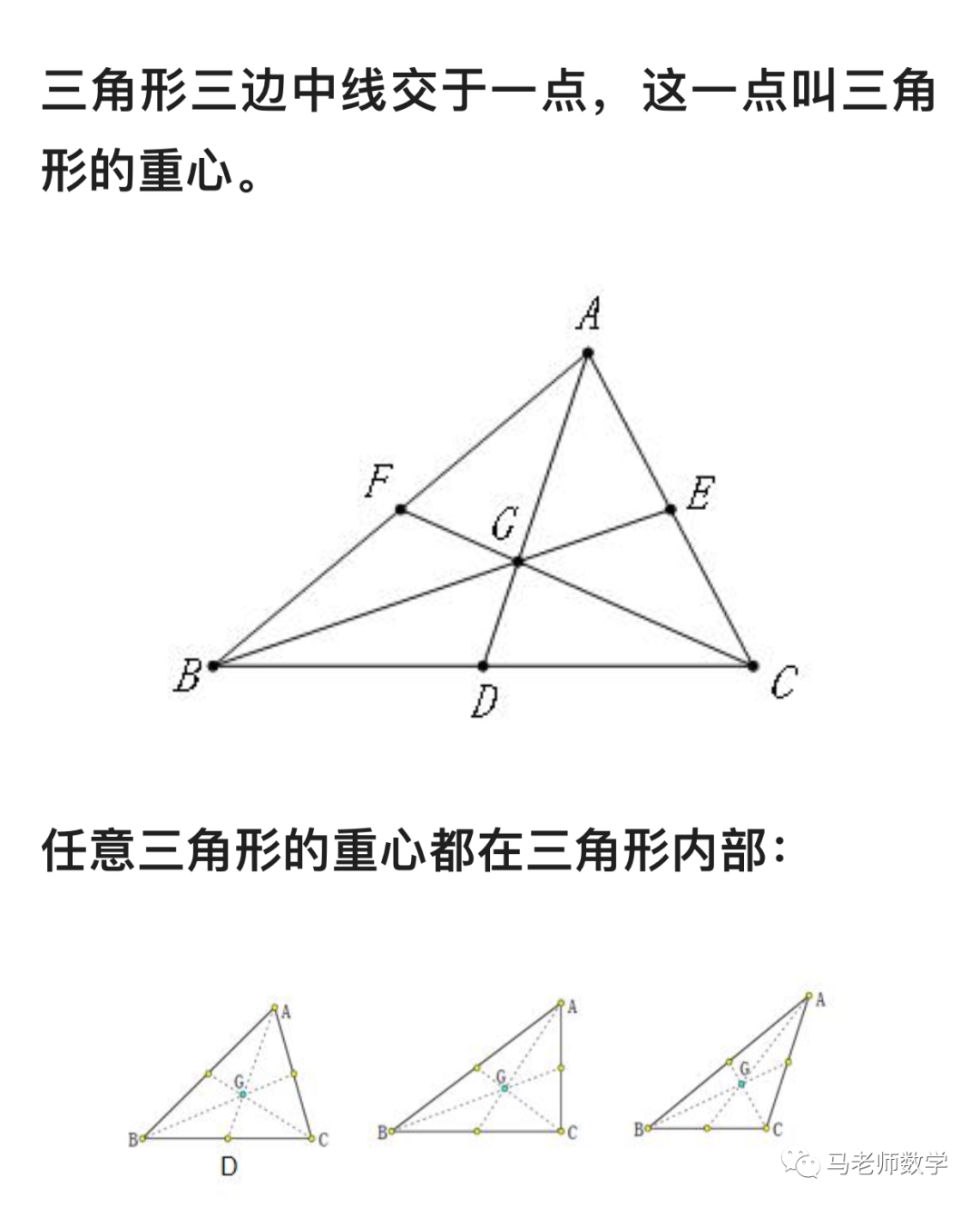
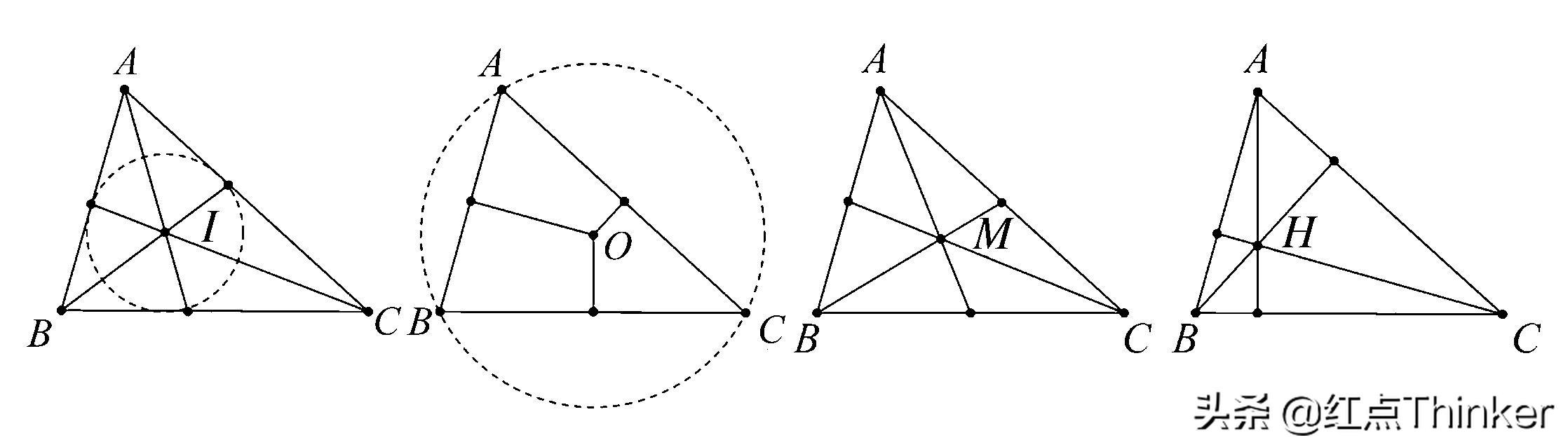
1、重心

重心是三角形三条中线的交点，其性质包括：

（1）重心到三角形的任意一边的中点的距离是重心到该边相对顶点的距离的一半。

（2）重心到三角形的三个顶点的距离之积与三角形的面积和它的外接圆的半径之积之间存在特定的数学关系。

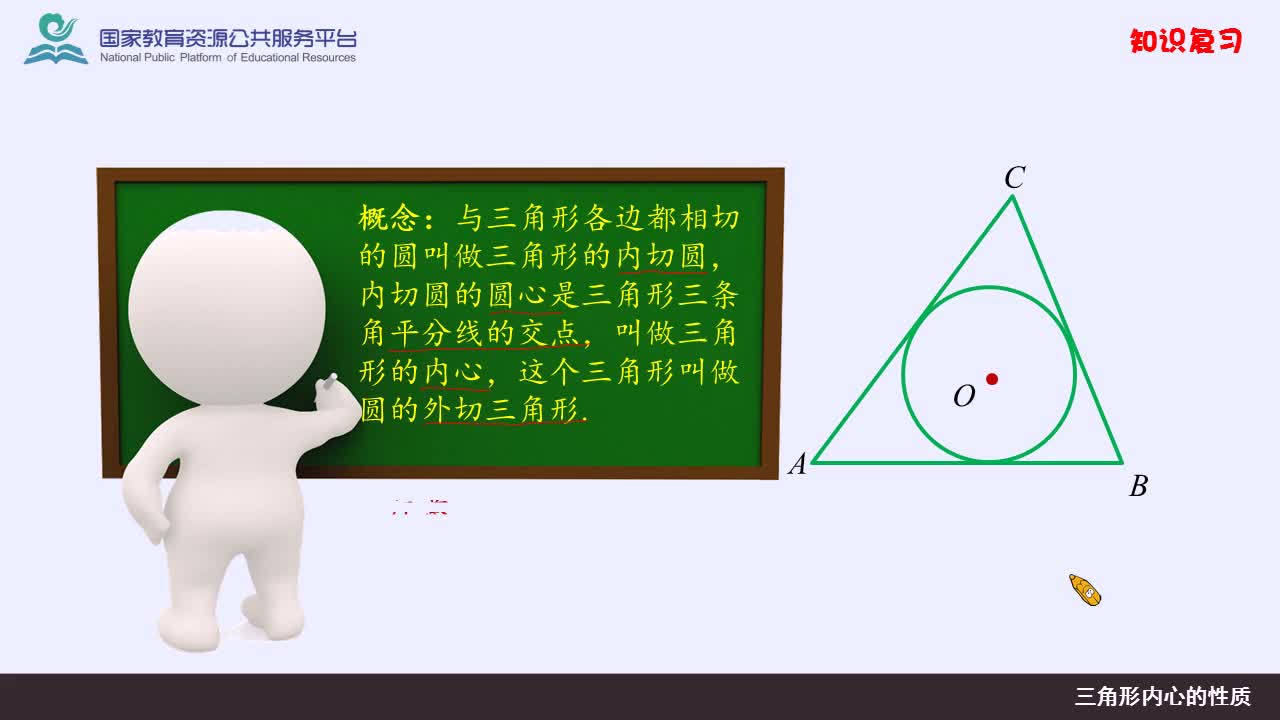
2、外心

外心是三角形三边的垂直平分线的交点，其关键性质为：

（1）外心到三角形三个顶点的距离相等，即三角形的外接圆的半径。

（2）外接圆的圆心与三角形的外心重合。

二、三角形中心的特点

除了上述的重心和外心，三角形还拥有内心和垂心等中心，这些中心共同构成了三角形独特的几何特性：

1、唯一性：每个三角形都具有唯一的外心、内心、重心和垂心，这些中心的位置由三角形的形状和大小唯一确定。

2、关联性：三角形的各个中心之间并非孤立存在，而是存在一定的关联性，重心、外心和垂心都位于三角形的特定线路上。

3、实用性：三角形中心的性质在实际生活中具有广泛的应用价值，在航海、建筑、静态力学等领域，三角形的外心和重心发挥着关键作用，在计算机图形学和图像处理等领域，三角形中心也具有重要的应用价值。

三、用户常见问题解答

在探讨三角形中心的过程中，许多读者可能会有以下疑问：如何计算三角形的重心？如何找到三角形的外心？内心和垂心的作用是什么？以下是针对这些问题的详细解答：

1、如何计算三角形的重心？

要计算三角形的重心，可以找出三条中线的交点，中线是连接一个顶点和它的对边中点的线段，通过计算每条中线并找到它们的交点，即可得到重心，在实际计算过程中，可以利用向量等方法简化计算过程，还可以通过计算机软件和工具轻松找到三角形的重心位置。

2、如何找到三角形的外心？

要找到三角形的外心，可以关注三边的垂直平分线的交点，通过找到每条边的垂直平分线并确定它们的交点，可以准确找到外心的位置，在实际操作中，可以利用尺规作图等方法来找到垂直平分线，根据三角形的边长等参数，也可以计算出外心的位置公式，掌握三角形外心的位置对于实际应用具有重要意义。

通过本文的介绍，相信读者对三角形中心的性质、特点以及常见问题有了更深入的了解，这些知识和技巧不仅有助于我们在实际生活中更好地运用三角形中心的性质来解决实际问题，还有助于提高文章在搜索引擎中的友好度和排名效果，从而更好地满足用户需求并促进知识传播和交流。