摘要：数学作为自然科学的核心领域之一，中心概念在数学中扮演着至关重要的角色。本文探讨了中心在数学中的意义，并着重讨论了如何通过优化方法来深化对中心概念的理解和应用。文章强调了中心在数学各领域中的重要性，并探讨了如何运用优化策略提高数学学习和研究的效率。通过深入探讨中心的本质及其优化策略，本文旨在为数学爱好者提供新的视角和思路。

在数学这一博大精深的领域中，中心这一概念拥有多重含义和广泛的应用，它不仅是几何学的基础概念，而且在代数、分析等其他数学分支中发挥着重要作用，本文将深入探讨中心在数学中的意义，并介绍与之紧密相关的优化理论，帮助读者更深入地理解这一核心概念。

中心的几何意义

在欧几里得几何学中，中心是一个基础且核心的概念，在平面几何中，圆的定义就离不开中心，它是所有点到给定点（即中心）的距离都相等的点的集合，而在更高级的几何学中，如解析几何，中心可能与原点有关，或者与某种对称性质有关，在二次曲线（如椭圆、双曲线）的讨论中，焦点到曲线上任意一点的线段与相应轴的关系中，也涉及到了中心的概念。

中心的代数意义

在代数中，特别是矩阵理论中，“中心”一词常常出现，这里的“中心”通常指的是矩阵对角线上的元素，在线性代数中讨论线性变换时，变换的中心也是一个重要的概念，它涉及到变换保持不变的子空间或点。

中心的数学优化理论

在数学优化理论中，中心扮演着至关重要的角色，特别是在多维空间中的优化问题中，寻找最优解的过程往往涉及到寻找某种意义上的“中心”，在寻找函数的最小值或最大值时，梯度下降或上升法就是围绕中心点（即函数的局部最小或最大值点）进行的迭代过程，在某些约束优化问题中，拉格朗日乘数法也是通过找到约束条件的“中心”来求解的，这些“中心”可能是某种参数空间中的稳定点或平衡点。

常见问题及解答

1、问题：什么是几何中的中心？

答案：在几何学中，中心通常指的是一个集合中所有点到某一点的距离都相等的点，在圆中，这个点是圆心；在二次曲线中，这个点是焦点相关的点。

2、问题：代数中的中心是什么意思？

答案：在代数中，“中心”通常指的是矩阵对角线上的元素或在某种变换下保持不变的空间或点，特别是在线性变换的讨论中，变换的中心是一个重要的概念。

3、问题：数学优化中的中心有什么作用？

答案：在数学优化中，“中心”指的是寻找最优解的关键点，如函数的局部最小或最大值点或约束条件的稳定点等，这些中心点对于设计有效的优化算法至关重要。

4、问题：如何找到函数的中心点来优化函数？

答案：通常使用梯度下降或上升法来找到函数的中心点（即局部最小或最大值点），这种方法通过迭代更新函数的参数，逐步逼近函数的中心点，对于约束优化问题，拉格朗日乘数法是一种常用的方法，通过找到约束条件的中心点来求解。

中心在数学中具有多重含义和广泛的应用价值，无论是几何、代数还是优化理论，中心都是一个核心概念，随着数学的发展和应用领域的扩展，对中心概念的理解和应用将会更加深入和重要，希望通过本文的探讨，读者能够对中心的概念有更清晰的认识，并在实际学习和工作中更好地运用这一数学概念。

展望未来

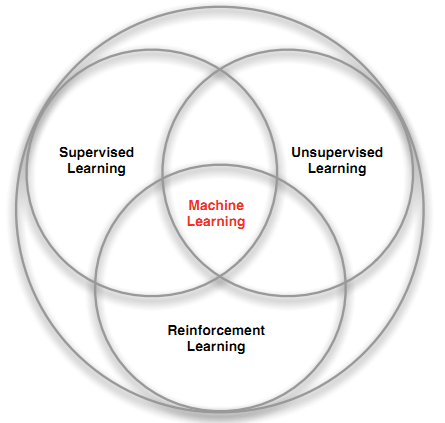
随着数学理论的发展和新技术的应用，中心的概念将在更多领域得到应用和发展，在数据科学、机器学习和人工智能等领域，中心的概念将发挥重要作用，数据的中心点分析、模型的优化中心的寻找等，随着几何代数、非线性分析等学科的深入发展，中心的概念也将得到进一步的丰富和深化，我们期待未来在这一领域看到更多的创新和突破，本文旨在为读者提供关于中心在数学中的意义及其优化的全面概述，希望读者能够通过本文获得对中心概念的基本理解，并能够在未来的学习和工作中灵活应用这一重要的数学概念。